ENSEMBLES (THÉORIE DES) - Théorie axiomatique

ENSEMBLES (THÉORIE DES) - Théorie axiomatique

La théorie des ensembles fut créée par Georg Cantor à la fin du XIX^e siècle. Cependant, le caractère extrêmement général et abstrait de la notion d’ensemble permit de produire des paradoxes rendant la théorie contradictoire (cf. théorie élémentaire des ENSEMBLES). Pour échapper à ces paradoxes et fournir un cadre abstrait adéquat au développement des mathématiques, le concept d’ensemble a dû être sérieusement codifié. Plusieurs théories formalisées des ensembles furent élaborées, en particulier: la théorie des types de Whitehead et Russell, la théorie des ensembles de Zermelo et Fraenkel, créée pour l’essentiel par Zermelo et enrichie par Fraenkel, et la théorie des classes de von Neumann, Bernays et Gödel. Malgré leurs différences, ces théories apparaissent avec le recul du temps comme diverses expressions d’une même réalité mathématique; ainsi, la théorie de Bernays et Gödel envisage des objets de deux types distincts (ensembles et classes), alors que la théorie de Zermelo et Fraenkel ne connaît que les ensembles; cependant, les énoncés relatifs aux ensembles seuls et démontrables par l’une ou l’autre théorie sont les mêmes. On va d’abord exposer ci-dessous la théorie de Zermelo-Fraenkel (désignée en abrégé par ZF) dont l’usage a fini par s’imposer aux spécialistes à la fois par son élégance conceptuelle et par son aptitude technique à élaborer en son sein la quasi-totalité des outils de la mathématique actuelle. Seront ensuite analysés les résultats d’indépendance: les travaux de Gödel puis ceux de Cohen, père du forcing, ont montré que le système de Zermelo-Fraenkel est insuffisant pour résoudre certains problèmes mathématiques, comme le célèbre problème du continu de Cantor. Ces résultats ont suscité un très important développement de la théorie axiomatique des ensembles dans les vingt dernières années, dont nous rendons compte plus loin, mais ils ont également remis en question l’objet de la théorie: deux voies s’ouvrent en effet. La première est celle d’un pluralisme ou d’un relativisme et consiste à étudier les divers modèles de la théorie des ensembles dans leur multiplicité. Selon ce point de vue, les résultats de Gödel et de Cohen s’analysent le plus naturellement comme des techniques permettant de passer d’un modèle de ZF à un autre vérifiant l’hypothèse du continu ou l’infirmant. L’autre voie consiste en la recherche de principes ensemblistes capables de fournir de nouveaux axiomes qui donnent la possibilité de répondre à des questions dont la théorie classique ne peut décider. Cette possibilité fut envisagée par Gödel lui-même avec la conviction que tout problème mathématique est susceptible d’une réponse déterminée.

Il se produit ici un phénomène intéressant et tout à fait spécifique: l’appréciation par les mathématiciens du domaine qu’ils explorent se trouve bouleversée par les techniques élaborées pour cette exploration. C’est ainsi que l’hypothèse du continu reste pour certains un problème ouvert qu’ils cherchent à résoudre par le recours à des principes nouveaux, alors que, pour d’autres, elle a cessé de constituer un problème mathématique digne d’intérêt.

Pour l’exposé des résultats de Gödel, de Cohen et d’autres, nous avons choisi le point de vue pluraliste, «modèle théorique», non pour imposer cette option mais parce qu’à notre avis on peut ainsi donner une meilleure idée de l’état d’avancement de la théorie, sans écarter la question de savoir si les recherches actuelles laissent entrevoir une réalisation au moins partielle du programme de Gödel.

1. Axiomes de ZF et procédés de formation d’ensembles

La théorie de Zermelo et Fraenkel est une théorie égalitaire du premier ordre dont les formules ne comportent – outre l’égalité – qu’un symbole de prédicat binaire noté 捻 (cf. Calcul des prédicats du premier ordre (Morphologie) in LOGIQUE MATHÉMATIQUE). Pour être simple, cette assertion n’en est pas moins susceptible de plusieurs interprétations.

D’un point de vue formaliste , les axiomes de la théorie ne sont que des assemblages de symboles de nature essentiellement typographique; la liste des axiomes donnée plus loin ne constitue qu’un procédé permettant de reconnaître si tel assemblage est ou non un axiome de ZF. Bien qu’étant assez proche – en définitive – du procédé adopté comme fondement dans les éléments de mathématiques de Bourbaki, le formalisme n’a essentiellement plus cours chez les spécialistes de théorie des ensembles; il se prête au demeurant fort mal à la présentation de cette théorie.

Le point de vue réaliste ou platonicien admet l’existence d’une collection d’objets 輪 appelés ensembles; les ensembles sont liés ou non par une relation notée 捻 et appelée relation d’appartenance ; si x et y sont des ensembles, on a donc:

(on dit alors que l’ensemble x appartient à l’ensemble y ou encore est élément de y ), ou bien:

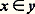
que l’on abrège en: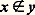

(on dit alors que l’ensemble x n’appartient pas à l’ensemble y ). À partir de là, on peut donner une valeur (vraie ou fausse) à chaque formule A du calcul des prédicats construit avec le symbole 捻, pour autant qu’on interprète chaque variable libre de A par un ensemble. En n’interprétant qu’une partie des variables libres de A par des ensembles, on obtient la notion de formule (ou énoncé) à paramètres ensembles.

Ce point de vue que nous adopterons pour la présentation de la théorie ZF nécessite en fait un minimum de pratique mathématique: manipulation sur les suites de symboles, usage des nombres entiers (pour définir, par exemple, le nombre de variables libres d’une formule). Les objets ainsi utilisés reçoivent le qualificatif d’intuitifs pour les distinguer de leurs analogues formels construits dans la collection d’objets 輪.

Ultérieurement, dans l’étude des résultats d’indépendance, nous utiliserons un autre point de vue, dit pluraliste , qui consiste en l’étude des divers modèles de ZF; une telle étude nécessite une pratique mathématique élaborée et de caractère ensembliste; nous y reviendrons.

Axiomes de Z

Axiome de l’ensemble vide

L’axiome de l’ensemble vide (1) exprime qu’il y a un ensemble dont aucun ensemble n’est élément. Un tel ensemble peut donc paraître comme le plus simple possible:

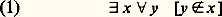Axiome d’extensionnalité

L’axiome d’extensionnalité (2) exprime que deux ensembles ayant les mêmes éléments sont égaux. On notera que la réciproque, à savoir que deux ensembles égaux ont les mêmes éléments, résulte des axiomes imposés à l’égalité (cf. Calcul des prédicats du premier ordre (Morphologie) in LOGIQUE MATHÉMATIQUE):

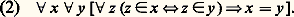Avant de poursuivre, observons que (2) garantit qu’il y a au plus un ensemble dont aucun ensemble n’est élément. Il résulte alors de (1) qu’il y a un seul ensemble , que l’on appellera l’ensemble vide et que l’on désignera par 歷, dont aucun ensemble n’est élément. Dans la suite, on s’attachera à construire d’autres ensembles en partant de 歷.

Axiome de la paire

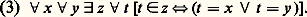L’axiome de la paire (3) exprime que, deux ensembles x et y étant donnés, il existe un ensemble z qui a pour seuls éléments x et y . Cet ensemble z , dont (2) garantit l’unicité, est désigné parx , y. En particulier, étant donné un ensemble x , il existe un ensemble désigné parx dont l’unique élément est x (appliquer l’axiome avec y = x ). On peut donc définir les ensembles:

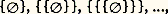ainsi que les ensembles:

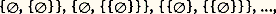on n’est pas encore en mesure d’affirmer l’existence d’un ensemble dont les seuls éléments seraient les ensembles 歷,歷參 et歷,歷參參. L’axiome suivant en fournira la possibilité.

Axiome de la réunion

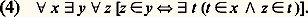L’axiome de la réunion (4) exprime que, pour tout ensemble x , il existe un ensemble y dont les éléments sont les éléments des éléments de x . Cet ensemble, nécessairement unique, est appelé réunion des éléments de x et est désigné par: face=F0019 聆 t .t 捻x

Étant donné un nombre fini (au sens intuitif) d’ensembles x ¹, x ², ..., x ^m , on peut alors montrer qu’il existe un ensemble (nécessairement unique), que l’on désigne parx ¹, ..., x ^m, dont les seuls éléments sont x ¹, ..., x ^m . Par exemple, l’ensemblex ¹, x ², x ³ n’est autre que l’ensemble: 聆 t , où 聆 t =索x ¹, x ²,x ³參.

t 捻X

On peut associer à chaque entier intuitif un ordinal fini :

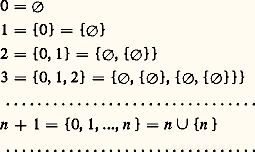(on notera que les éléments de cette suite sont distincts).

Étant donné des ensembles x ¹, x ², ..., x ⁿ , on désigne par:

et on appelle réunion des ensembles x ⁱ l’ensemble: face=F0019 聆 t , où X =x ¹, x ², ..., x ⁿ. t 捻X

Axiome de l’ensemble des parties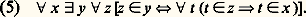

Étant donné des ensembles z et x , on dira que z est une partie ou un sous-ensemble de x et on écrira z 說 x si tout élément de z est un élément de x . L’axiome de l’ensemble des parties (5) peut alors être abrégé en:

Cet axiome exprime que, pour tout ensemble x , il existe un ensemble y ayant pour (seuls) éléments les parties de x . Cet ensemble est appelé ensemble des parties de x et est désigné par 戮(x ). Ainsi, par exemple, on a 1 = 戮(0), 2 = 戮(1), 3 戮(2).

Axiome de l’infini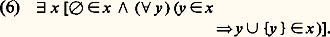

Tous les ensembles que l’on peut construire à l’aide des axiomes (1) à (5) ont, au sens intuitif, un nombre fini d’éléments. L’axiome de l’infini (6) garantit l’existence d’un ensemble dont tout ordinal fini est élément et qui aura donc, au sens intuitif, un nombre infini d’éléments. Il va de soi que, si l’on était assuré que la collection des ordinaux finis constitue un ensemble, l’axiome (6) serait superflu. Il résulte, en fait, de l’axiome (6) et du schéma d’axiomes (7) que la collection des ordinaux finis constitue bien un ensemble.

Schéma de compréhension

Le schéma de compréhension (Aussonderung en allemand, separation en anglais) exprime que, pour tout ensemble x et tout énoncé A(z , x ¹, ..., x ^k ) à une variable libre z et à paramètres x ¹, ..., x ^k , il existe un ensemble y dont les éléments sont ceux des éléments de x qui satisfont l’énoncé A. Le schéma de compréhension consiste donc en la liste infinie des axiomes suivants (un pour chaque énoncé A):

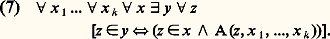Le schéma de compréhension permet de construire de nouveaux ensembles à partir d’ensembles déjà construits . On va indiquer un schéma plus puissant.

Schéma de remplacement

Considérons un énoncé A(x , y , x ¹, ..., x ^k ) à paramètres x ¹, ..., x ^k ; on dit que A définit une relation fonctionnelle à un argument ou, plus brièvement, que A est fonctionnel si, notant 倫(x , y ) pour A(x , y , x ¹, ..., x ^k ), on a: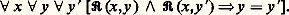

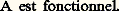La ligne précédente représente un énoncé portant sur x ¹, ..., x ^k qu’on symbolisera par:

Le schéma de remplacement consiste en la liste infinie des axiomes suivants (un pour chaque énoncé A):

Autrement dit, pour tout ensemble y , il existe un ensemble z dont les éléments sont exactement les images, par la relation fonctionnelle considérée, des éléments de y .

On adoptera la terminologie suivante: Z désigne la théorie du premier ordre ayant pour axiomes les axiomes (1) à (7) et Z^- la théorie du premier ordre ayant pour axiomes les axiomes (1) à (6) et (8); on réserve la notation ZF à la théorie obtenue en adjoignant à Z^- l’axiome de fondation (10) qui sera introduit au chapitre 3 et la notation Z^-C (resp. ZFC) à la théorie obtenue en adjoignant à Z^- (resp. ZF) l’axiome du choix (9) qui sera introduit au chapitre 2. On laisse au lecteur le soin de vérifier que Z^- est une théorie plus forte que Z, de vérifier plus précisément que (7) est une conséquence immédiate de (8).

Procédés de formation d’ensembles

Dans la suite de ce chapitre, on indiquera rapidement les procédés courants de fabrication d’ensembles: produit, réunion, intersection...

Étant donné des ensembles x et y , on désigne par (x ,y ) et on appelle couple de x et y l’ensemble索x,x , y參. Il est clair que:

et on vérifie facilement qu’on a, étant donné des ensembles x , x , y , y :

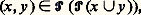
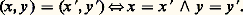Soient u et v des ensembles. On appelle produit de u et v et on désigne par u 憐 v l’ensemble des couples (x ,y ) tels que x 捻 u et y 捻 v ; qu’il s’agisse bien d’un ensemble résulte de (7). On appelle application de u dans v toute partie a de u 憐 v telle que l’énoncé: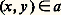

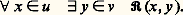définisse une relation fonctionnelle notée 倫(x , y ) et telle que l’on ait:

L’unique élément y associé par 倫 à un élément x de u est appelé image de x par a . Toute application de u dans v étant un élément de 戮(u 憐 v ), on peut, grâce à (7), considérer l’ensemble de toutes les applications de u dans v que l’on désigne par v ^u . L’application 﨏 de 2^u dans 戮(u ), qui à toute application 倫 de u dans 2 associe 﨏( 倫) =x 捻 u | 﨏(x ) = 0, permet d’identifier 2^u à 戮(u ). Autrement dit, c’est une application bijective.

Il sera commode d’employer les notations suivantes:

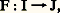qui désignera le fait que F est une application de l’ensemble I dans l’ensemble J;

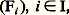qui désignera le fait que F est une application de l’ensemble I dans un ensemble non précisé. Pour tout élément i de I, l’image de i par F est désignée ici par Fⁱ ; on dira alors que (Fⁱ ), i 捻 I, est une famille d’ensembles.

On appelle réunion de la famille (Fⁱ ), i 捻 I, et on désigne par: face=F0019 聆 Fⁱ la réunion i 捻Ides éléments de l’image de la fonction F. Puisque l’image de la fonction F est, en vertu de (8), un ensemble, il résulte de (4) que: face=F0019 聆 Fⁱ constitue bien un ensemble. On i 捻Inotera que la réunion de la famille vide (I = 歷) n’est autre que l’ensemble vide.

Si I n’est pas vide, on appelle intersection de la famille (Fⁱ ), i 捻 I, l’ensemble des éléments x tels que, pour tout i 捻 I, x est élément de Fⁱ . On désigne cet ensemble par: face=F0019 惡 Fⁱ .i 捻I

Considérons maintenant la collection des applications: f : I聆 Fⁱ telles que i 捻If (i ) 捻 Fⁱ pour tout i 捻 I. Tout élément de cette collection étant un élément de l’ensemble: (face=F0019 聆 Fⁱ )^I, il résulte facilement de i 捻Ide (7) que cette collection constitue un ensemble que l’on désigne par:

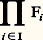et que l’on appelle produit de la famile Fⁱ . On laisse au lecteur le soin de vérifier que cette définition généralise bien celle du produit u 憐 v de deux ensembles et celle de l’ensemble v ^u .

Pour conclure ce chapitre, il est utile de préciser l’apport de la théorie axiomatique des ensembles dans l’élimination des paradoxes. Tout énoncé A(x , x ¹, ..., x ^k ) à une variable libre et à paramètres x ¹, ..., x ^k définit une collection d’ensembles formée de ceux qui satisfont A. On peut donner des exemples de collections qui ne sont pas des ensembles. Un tel exemple est fourni par le «paradoxe» bien connu de Russell: Soit C la collection des ensembles x tels que x 殮 x ; si C constituait un ensemble, on aurait 葉 x (x 殮 x 沈 x 捻 C), et donc en particulier C 殮 C 沈 C 捻 C, ce qui est absurde.

Le paradoxe de Russell est ainsi devenu un théorème intéressant et inoffensif de la théorie des ensembles.

2. Ordinaux et cardinaux. Axiome du choix

L’étude des ordinaux puis des cardinaux est fondamentale en théorie des ensembles car elle explicite la notion d’itération illimitée d’un même procédé, qui fut à la base des découvertes de Cantor. Elle permet également de résoudre les deux problèmes suivants.

(A) Trouver une relation fonctionnelle associant à chaque ensemble bien ordonné x un ensemble h ^x de façon que deux ensembles bien ordonnés x et y soient isomorphes (c’est-à-dire qu’il existe une bijection croissante de x sur y ) si et seulement si h ^x = h ^y .

(B) Trouver une relation fonctionnelle associant à chaque ensemble x un ensemble k ^x de façon que x et y soient en bijection si et seulement si k ^x = k ^y .

La théorie des ordinaux fournit la solution du premier problème et celle des cardinaux fournit celle du second, moyennant l’usage de l’axiome du choix qui sera décrit plus loin. Il est impossible de résoudre le problème (B) dans Z^-, mais on verra au chapitre 3 que l’axiome de fondation permet une théorie des cardinaux en l’absence d’axiome du choix.

Les ordinaux

L’axiome de l’infini (6) garantit l’existence d’un ensemble x tel que l’on ait:

Appelons inductif un tel ensemble. On démontre facilement l’existence d’un plus petit ensemble inductif qu’on note 諸. 諸 contient tous les ordinaux finis associés aux entiers intuitifs (cf. chap. 1), mais ces derniers n’ont aucune raison d’épuiser 諸. Les éléments de 諸 sont notés par les lettres m , n , ...; on écrit m 麗 n pour m 捻 n , ce qui définit une relation d’ordre strict sur 諸. On écrit n + 1 pour n 聆n; n + 1 est successeur immédiat de n . La définition de 諸 permet de formaliser la notion de définition par récurrence.

Théorème. Soit X un ensemble, u un élément de X, f une application de X dans lui-même; il existe une unique application g de 諸 dans X telle que: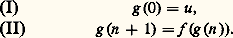

La découverte fondamentale de Cantor est que la récurrence n’épuise pas les possibilités d’itération. Considérons l’application qui à un fermé F de la droite réelle associe le fermé F obtenu en privant F de ses points isolés et appelé fermé dérivé. Par récurrence, on définit ⁽ⁿ⁾ de façon que:

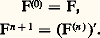On obtient ainsi une suite décroissante de fermés. Il est naturel de considérer le fermé:

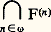et d’attacher ce fermé à l’ensemble 諸. Par dérivation, on obtient un nouveau fermé qu’on peut attacher à l’ensemble 諸 + 1 = 諸 聆 諸; on est ainsi amené à introduire les nombres transfinis 諸 + 1, 諸 + 2, ... ce qui conduit à 諸 + 諸 = 諸 + n : n 捻 諸. La définition globale qui suit épuise ce processus:

On dit qu’un ensemble 見 est un ordinal si les deux conditions suivantes sont réalisées :

(I) 見 est transitif ; ce qui signifie que tout élément de 見 est une partie de 見.

(II) la relation binaire 麗 définie sur 見 par :

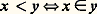est une relation de bon ordre strict .

Il est facile d’écrire une formule On (x ) à une variable libre qui est satisfaite par les ordinaux et seulement par eux. On peut donc parler de la collection des ordinaux.

On établit alors les résultats suivants:

a) Pour tout ordinal 見, on a 見 殮 見.

b) Si 見 est un ordinal, 見 聆 見 est un ordinal noté aussi 見 + 1 et appelé successeur de 見.

c) 諸 est un ordinal mais n’est pas un successeur; on dit que c’est un ordinal limite .

d) Tout élément d’un ordinal est un ordinal.

e) Si 見 et 廓 sont des ordinaux distincts, on a 見 捻 廓 (qu’on écrit 見 麗 廓) ou bien 廓 捻 見.

On vient de voir que la relation d’appartenance permet de comparer des ordinaux distincts, ce qui donne un sens à:

f) Tout ensemble non vide d’ordinaux a un plus petit élément.

La collection des ordinaux n’est pas un ensemble; sinon, cet ensemble x serait transitif (par d) et bien ordonné par 捻 (d’après e et f); x serait donc un ordinal; on aurait par ailleurs x 捻 x , ce qui contredit a.

La propriété f s’étend aux collections, ce qui fonde le principe de démonstration par induction transfinie: pour établir qu’une collection C contient tous les ordinaux, il suffit de vérifier que tout ordinal inclus dans C est élément de C. Pour établir ce principe on raisonne par contradiction en considérant un élément minimal de la collection On 漣C.

Énonçons maintenant le principe d’induction transfinie qui est la condition sine qua non du développement de la théorie.

Théorème . Soit F une relation fonctionnelle de domaine la collection des fonctions définies sur un ordinal; il existe une relation fonctionnelle G de domaine la collection des ordinaux et telle que pour tout ordinal 見:

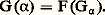Note : dans ce qui précède, G size=1^見 désigne la fonction que G définit par restriction à 見; le domaine d’une relation fonctionelle F est la collection des ensembles qui ont une image par F.

La preuve de ce principe repose sur l’écriture soigneuse d’une formule définissant G à partir d’une formule définissant F et sur l’usage du principe de démonstration par induction transfinie.

On va maintenant établir le théorème suivant, qui résout le problème (A) énoncé précédemment.

Théorème . Tout ensemble bien ordonné est isomorphe à un unique ordinal.

Preuve . La démonstration de l’unicité est facile et – au demeurant – peu instructive; nous nous bornerons à examiner la preuve de l’existence de l’isomorphisme. Soit X un ensemble bien ordonné; on fixe un ensemble p qui n’appartient pas à X (il en existe!) et on définit par induction transfinie une relation fonctionnelle F telle que:

F( 見) est le plus petit élément de X qui n’appartient pas à l’image de F size=1^見, s’il en existe;

F( 見) = p sinon.

Il est aisé d’établir par induction transfinie que si F( 見) est différent de p , F size=1^見 est une injection croissante de 見 sur un segment initial de X. Si donc p n’est pas atteint, F définit une relation fonctionnelle injective de domaine les ordinaux à valeurs dans X et la relation fonctionnelle G inverse de F définit une surjection d’une partie de X sur la classe des ordinaux, ce qui contredit le schéma de remplacement.

Si maintenant 見⁰ est le plus petit ordinal tel que F( 見⁰) = p , F size=1^見0 est l’isomorphisme cherché.

On observe l’utilisation du schéma de remplacement; de fait, le théorème ci-dessus ne peut être établi dans la théorie Z.

Le principe de définition par induction transfinie permet également de développer une arithmétique des ordinaux; on se contentera ici de définir la somme de deux ordinaux.

Étant donné un ordinal 見, on définit la relation fonctionnelle S size=1^見( 廓) par:

La somme 見 + 廓 est alors définie par S size=1^見( 廓).

Les cardinaux et l’axiome du choix

Étant donné des ensembles x et y , on dira que x et y sont équipotents s’il existe une bijection de x sur y .

Théorème de Cantor. Pour tout ensemble x , les ensembles x et 戮(x ) ne sont pas équipotents.

Démonstration. Supposons au contraire qu’il existe une bijection f de x sur 戮(x ). Désignons par y la partie de x ayant pour éléments tous les éléments z de x tels que l’on ait z 殮 f (z ). Puisque f est surjective, il existe u 捻 x tel que f (u ) = y . Alors: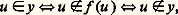

ce qui est une contradiction.

Théorème de Cantor-Bernstein. Étant donné des ensembles x et y , s’il existe une injection de x dans y et une injection de y dans x , alors x et y sont équipotents.

Le théorème de Cantor-Bernstein, dont nous ne donnons pas la preuve, permet de développer dans la théorie Z^- une partie de la théorie des cardinaux. Ce sujet étant assez technique, nous préférons introduire maintenant l’axiome du choix .

(9) Pour tout ensemble x il existe une application de l’ensemble des parties non vides de x dans x qui à tout élément z de 戮(x ) 漣歷參 associe un élément h (z ) de z.

Théorème (de ZF^-C) . Le produit d’une famille d’ensembles non vides est non vide.

Démonstration : Soit (x ⁱ ), i 捻 I, une famille d’ensembles non vides. Appliquons (9) à l’ensemble:

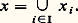Nous obtenons une application h de 戮(x ) 漣歷參 dans x qui, en particulier, associe à chacun des x ⁱ un élément h (x ⁱ ) de x ⁱ . L’application:

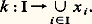définie par:

est un élément du produit de la famille (x ⁱ ), i 捻 I.

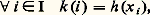Théorème du bon ordre. Tout ensemble peut être bien ordonné (il s’agit d’un théorème de Z^-C).

Observons d’abord que la conclusion du théorème entraîne immédiatement dans Z^- l’axiome du choix: en effet, si R est une relation de bon ordre sur l’ensemble x , l’application h de 戮(x ) 漣歷參 dans x , qui à tout y appartenant à 戮(x ) 漣歷參 associe le plus petit élément h (y ) de y , satisfait bien la condition:

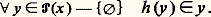Pour établir le théorème, nous nous donnons un ensemble x et une application h de 戮(x ) 漣歷參 dans x telle que h (y ) 捻 y pour toute partie non vide y de x et nous allons montrer qu’il existe une relation de bon ordre sur x .

Soit p un ensemble qui n’est pas élément de x ; définissons par induction transfinie une relation fonctionnelle F de domaine On à valeurs dans x 聆p en posant: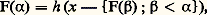

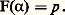si l’ensembleF( 廓); 廓 麗 見 est une partie de x distincte de x . Sinon:

Supposons que F( 見) 捻 x pour tout ordinal 見. Il résulte alors que, pour tout ordinal 見, on a:

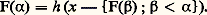Par définition même de h , l’élément F( 見) est distinct de tous les éléments F( 廓) pour tout 廓 麗 見. Autrement dit, la relation fonctionnelle F de domaine On et à valeurs dans x est injective. La relation fonctionnelle F induit donc une bijection F de On sur un sous-ensemble x de x . En appliquant le schéma de remplacement à la bijection réciproque de F , on déduit que les ordinaux forment un ensemble, d’où une contradiction. Soit maintenant 見⁰ le plus petit ordinal tel que F( 見⁰) = p ; il est facile de voir que F size=1^見0 réalise une bijection de 見⁰ sur x , ce qui permet de transporter sur x la relation de bon ordre de 見⁰.

La démonstration est maintenant terminée. On vient d’établir, grâce à l’axiome du choix, que tout ensemble est équipotent à un ordinal. On appellera cardinal d’un ensemble x et on désignera par Card(x ) le plus petit ordinal équipotent à x . Tout ordinal fini est un cardinal et 諸 est le plus petit cardinal infini. Tout cardinal infini est un ordinal limite.

Il est clair que deux ensembles sont équipotents si et seulement si ces deux ensembles ont même cardinal . Il est assez facile de voir que la collection des cardinaux n’est pas un ensemble. Plus précisément, il existe une relation fonctionnelle 尿 de la collection On sur la collection des cardinaux infinis qui est bijective et qui préserve l’ordre de On. L’élément 尿 (0) n’est autre que le premier cardinal infini, à savoir 諸. L’élément 尿 (1) est le plus petit ordinal strictement supérieur à 尿 (0). On note habituellement 尿 size=1^見 au lieu de 尿 ( 見).

L’hypothèse du continu est l’énoncé:

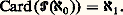Elle n’est ni réfutable ni démontrable dans ZFC, et on examinera plus loin les preuves qui permettent d’obtenir ce résultat d’indépendance.

L’hypothèse généralisée du continu est l’énoncé:

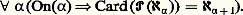On peut développer une arithmétique des cardinaux qui ne coïncide pas avec celle des ordinaux mais qui – en présence de l’axiome du choix – est bien simple. Si on définit le produit de deux cardinaux comme le cardinal de leur ensemble produit, on constate que le produit de deux cardinaux infinis est égal au plus grand des deux. On démontre aussi à l’aide de l’axiome du choix le résultat suivant:

Théorème. Soit 見 un cardinal et (Xⁱ ); i 捻 I une famille d’ensemble de cardinal 諒 見, indexée par un ensemble I de cardinal 諒 見, alors l’ensemble:

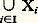est aussi de cardinal 諒 見.

L’une des caractéristiques les plus importantes d’un cardinal est sa cofinalité . Soit 見 un cardinal et X une partie de 見; on dit que X est cofinale si sup X = 見, c’est-à-dire si 見 est le plus petit ordinal supérieur à tous les éléments de X. La cofinalité de 見 est le plus petit cardinal tel que 見 ait une partie cofinale de cardinal . Un cardinal est régulier s’il est égal à sa cofinalité, singulier s’il est strictement supérieur à sa cofinalité. On démontre à l’aide du théorème précédent que tout cardinal de la forme 尿 size=1^見+1 est régulier; le plus petit cardinal singulier est 尿 size=1^諸. Un cardinal est dit faiblement inaccessible s’il est régulier sans être de la forme 尿 size=1^見+1; fortement inaccessible (ou simplement inaccessible) si, de plus, pour tout cardinal 麗 , on a:

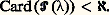L’existence des cardinaux inaccessibles ne peut être établie dans ZFC; nous entrons là dans l’étude des grands cardinaux, qui a constitué une des voies de recherches privilégiées dans les tentatives de renforcer le système ZFC; nous y reviendrons au chapitre 8.

Avant de poursuivre l’étude de la théorie des ensembles, examinons le rôle joué par l’axiome du choix en mathématiques; ce dernier intervient le plus souvent par l’intermédiaire de l’énoncé suivant qui lui est équivalent (dans ZF^-):

(9 ) Lemme de Zorn . Soit X un ensemble ordonné non vide; on suppose que toute partie totalement ordonnée (pour l’ordre induit) admet un majorant; alors X a un élément maximal.

C’est à l’aide du lemme de Zorn que l’on démontre l’existence d’ultrafiltres non triviaux, de la clôture algébrique d’un corps, de certaines formes linéaires continues dans les espaces normés (théorème de Hahn-Banach), etc. Ces démonstrations ne conduisent pas à une définition explicite de l’objet dont elles assurent l’existence; cela explique sans doute en partie les controverses suscitées par le caractère non «constructif» de cet axiome ^{[cf. INTUITIONNISME]}. Ces controverses sont pour l’essentiel aujourd’hui éteintes; il n’en reste pas moins qu’une partie des mathématiques peut être construite sans recours à l’axiome du choix ou en n’utilisant que des versions affaiblies de cet axiome. C’est ainsi que la théorie de la mesure nécessite l’utilisation d’un minimum de choix (ne serait-ce que pour démontrer que R n’est pas réunion dénombrable d’ensembles dénombrables), mais peut être développée en n’utilisant que l’axiome des choix dépendants qui s’énonce ainsi: si une relation binaire est telle que tout élément de son domaine est lié au moins à un autre, il existe une suite d’éléments chacun lié au suivant.

Les travaux de Gödel et de Cohen ont montré l’indépendance de l’axiome du choix, mais ont aussi permis de hiérarchiser diverses conséquences de cet axiome; cette question sera reprise au chapitre 6.

3. Hiérarchie des ensembles et axiome de fondation

Les résultats du chapitre précédent permettent de définir par induction transfinie la relation fonctionnelle V suivante, de domaine On:

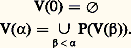Il est alors facile d’établir les résultats suivants:

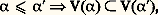pour tous ordinaux 見 et 見 ;

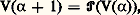pour tout ordinal 見;

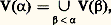pour tout ordinal limite 見.

Désignons par V la collection ayant pour éléments tous les ensembles x pour lesquels il existe un ordinal 見 tel que x 捻 V( 見). Les V( 見) constituent une stratification de V, à laquelle on donne souvent le nom de hiérarchie cumulative des ensembles (cumulative, car contrairement à ce que l’on a dans la théorie des types, chaque V( 見) est contenu dans les V( 見 ) suivants). On notera désormais, conformément à l’usage, V size=1^見 au lieu de V( 見). On peut établir que les axiomes de Z^- (resp. de Z^-C) restent valides quand on les interprète dans V (en donnant un sens précis à cette notion d’interprétation). Il est alors naturel de chercher à limiter les ensembles à la collection V. Il est remarquable que, pour obtenir ce résultat, il suffise d’adjoindre à Z^- l’axiome suivant, dit axiome de fondation puisqu’il entraîne que tout ensemble est construit à partir de l’ensemble vide:

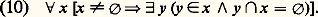Cet axiome exprime que tout ensemble non vide a un élément qui n’a aucun élément commun avec cet ensemble. Si l’on admet (9), ou au moins si l’on admet l’axiome des choix dépendants, il est facile de voir que (10) peut s’énoncer de la façon suivante.

(10 ) Il n’existe pas de relation fonctionnelle f de domaine 諸 telle que, pour tout entier n, on ait :

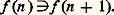L’une des conséquences de (10) est qu’il n’y a pas d’ensemble x tel que x =x ou même tel que x 捻 x .

L’adjonction de l’axiome de fondation n’est pas dangereuse: la théorie ZF (resp. ZFC) est non contradictoire si et seulement si Z^- (resp. Z^-C) l’est; à première vue, elle peut cependant apparaître superflue et l’élimination des ensembles pathologiques qui appartiennent à eux-mêmes est une justification un peu mince. De fait, la véritable raison qui a conduit à l’adoption de cet axiome est de nature métamathématique: il enrichit la théorie de nouveaux principes qui sont indispensables dans l’étude des résultats d’indépendance.

Tout d’abord, appelons rang d’un ensemble x le plus petit ordinal 見, s’il existe, tel que x 捻 V size=1^見; l’axiome de fondation permet d’assigner un rang à chaque ensemble et autorise ainsi des principes de construction ou de démonstration par «induction sur le rang», utilisés par exemple dans la méthode de Cohen.

L’axiome de fondation permet d’établir le principe de réflexion: si 淋 (x ^l, ..., x ⁿ ) est un énoncé à n variables libres, il existe des ordinaux 見 arbitrairement grands tels que:

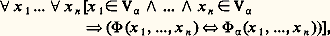où 淋 size=1^見 désigne l’interprétation de 淋 dans V size=1^見. On verra ultérieurement où intervient le principe de réflexion.

Signalons enfin que l’axiome de fondation permet de définir une notion de cardinal même en l’absence de l’axiome du choix. À tout élément x , on associe l’ensemble k ^x des ensembles équipotents à x de rang minimal. Il est facile de voir qu’on obtient ainsi une solution du problème (B) (cf. chap. 2).

4. Les limites de ZF

Ainsi qu’on l’a mentionné à plusieurs reprises, l’axiome du choix ne peut être décidé dans ZF et, de même, l’hypothèse du continu ne peut être décidée dans ZFC, plus précisément:

Théorème.

(I) Si la théorie ZF est non contradictoire, alors la théorie ZFC est non contradictoire et aussi la théorie ZFC augmentée de l’hypothèse du continu.

(II) Si la théorie ZF est non contradictoire, alors la théorie ZF augmentée de la négation de l’axiome du choix est non contradictoire; de même, pour la théorie ZFC à laquelle on adjoint la négation de l’hypothèse du continu.

La partie I est due à Gödel (1938) et la partie II à Cohen (1963). Avant de présenter les techniques utilisées dans les preuves, il paraît utile de réfléchir à la nature mathématique de résultats tels que I et II, qu’on appelle résultats de non-contradiction relative . Tout d’abord, rappelons que le théorème d’incomplétude de Gödel exclut toute démonstration de non-contradiction absolue: on ne peut établir dans ZF que ZF est non contradictoire et cela vaut également pour toutes les variantes de ZF ^{[cf. LOGIQUE MATHÉMATIQUE]}. Par ailleurs, il est tentant, pour comprendre la notion de non-contradiction relative, d’invoquer le théorème de complétude ; bornons-nous, dans la discussion, à examiner la non-contradiction relative de ZFC; par complétude, celle-ci se trouve établie dès qu’on a fourni une méthode permettant de passer d’un modèle face=F9828 M de ZF à un modèle face=F9828 M de ZFC. Comme nous l’avons mentionné dans l’introduction de cet article, cela conduit à une conception pluraliste de la théorie des ensembles et à l’étude de ses divers modèles. Cependant, la démonstration de la non-contradiction relative de ZFC esquissée plus haut n’est pas satisfaisante au niveau des fondements: seule est acceptable une méthode effective permettant d’associer à toute preuve formelle d’une contradiction à partir des axiomes de ZFC une autre n’utilisant que les axiomes de ZF; une telle méthode est dite finitiste. Pour justifier malgré tout l’adoption du point de vue pluraliste, qui conduit à un exposé plus clair et plus convaincant, nous nous contenterons de dire que tout résultat de non-contradiction relative obtenu par ce point de vue est susceptible d’une traduction finitiste.

Avant de passer à l’étude des résultats d’indépendance, il convient de souligner qu’il existe des hypothèses pour lesquelles il ne peut y avoir de démonstration de non-contradiction relative. Une telle hypothèse est dite plus forte que ZF. Bien évidemment, si H est plus forte que ZF, H n’admet pas de preuve dans ZF; la situation est alors la suivante: il se peut qu’il existe une preuve de la négation de H, mais, s’il n’en existe pas, il n’existe aucun moyen mathématique de s’en assurer. Admettre qu’une telle hypothèse est vraie, ou simplement en étudier les conséquences, relève donc de l’intuition mathématique.

Un exemple d’hypothèse qui soit plus forte que ZF est celle de l’existence d’un cardinal inaccessible qu’on notera HI. Si 見 est un cardinal inaccessible, V size=1^見 est un modèle de ZF; par le théorème d’incomplétude, HI n’est pas prouvable dans ZF (sauf si ZF est contradictoire). Une variante de cette preuve montre que la non-contradiction relative de HI ne peut être obtenue non plus. On observe de façon analogue que V size=1^諸+ size=1^諸 est un modèle de Z, ce qui conduit à dire que Z^- est plus forte que Z.

Nous adoptons désormais le point de vue pluraliste. La considération simultanée de plusieurs modèles à laquelle nous sommes conduits ne rompt pas l’unité des développements élémentaires de la théorie des ensembles, ni du reste celle des mathématiques. En effet, les constructions des ordinaux, des cardinaux, des nombres réels, etc. sont uniformes (en ce sens qu’elles sont définies par une même formule dans les divers modèles). Qu’on ne s’y méprenne pas cependant: les énoncés indépendants (de ZF) ne sont pas d’une complexité qui les vide de tout contenu intuitif; on peut en donner des exemples dans de nombreuses branches de mathématiques, ainsi qu’on le verra plus loin. De même, l’étude de modèles de versions renforcées de ZF ne concerne pas seulement les fondements: certaines hypothèses sur les cardinaux affectent la structure de certains objets très «concrets», comme les ensembles de nombres réels.

5. Construction de modèles de ZF

Dans cette section, on va présenter plusieurs techniques permettant de passer d’un modèle face=F9828 M de ZF à un autre face=F9828 M : ensembles constructibles, ensembles définissables à partir d’ordinaux, extensions génériques. Pour chaque construction, on s’est attaché à donner un résultat global fournissant une définition précise de face=F9828 M à partir de face=F9828 M, mais laissant de côté les détails de la construction proprement dite de face=F9828 M , lesquels nécessiteraient de longs développements.

Modèles intérieurs; ensembles constructibles

Soit face=F9828 M un modèle de ZF. On rappelle qu’un tel modèle est la donnée d’une collection d’objets M munie d’une relation binaire E, appelée relation d’appartenance du modèle. Une partie X de M est un modèle intérieur de face=F9828 M si les conditions suivantes sont satisfaites:

– X contient les ordinaux de face=F9828 M,

– X est transitive (tout objet qui appartient au sens de face=F9828 M à un élément de X est aussi élément de X),

– le modèle obtenu en munissant X de la restriction de E à X est un modèle de ZF.

La recherche de modèles intérieurs minimaux conduit immédiatement à la notion d’ensemble constructible.

Théorème . Soit face=F9828 M un modèle de ZF. Il existe un plus petit modèle intérieur de face=F9828 M noté L face=F9828 M. De plus, il existe un énoncé L (v ) à une variable libre v, indépendant du modèle face=F9828 M qui permet de définir L face=F9828 size=1^M dans face=F9828 M.

L’énoncé L (v ) se lit «v est constructible». L face=F9828 size=1^M est formé des objets a de M qui sont constructibles dans face=F9828 M, c’est-à-dire qui sont tels que L(a ) soit vrai dans face=F9828 M.

La notion d’ensemble constructible est due à Kurt Gödel (1938); il est bien évident que la partie difficile de la preuve du théorème ci-dessus correspond à la construction explicite de L face=F9828 size=1^M dans face=F9828 M. Plusieurs choix sont possibles. L’un deux, inspiré de la construction inventée initialement par Gödel, a été mis à l’honneur par les travaux de R. B. Jensen, que nous analyserons au chapitre 8; il est fondé sur l’utilisation des fonctions de Gödel qui sont les relations fonctionnelles suivantes:

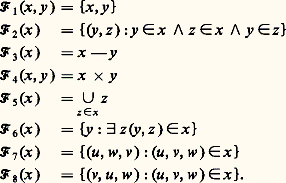Le triplet (u ,v ,w ) est, par définition, le couple (u , (v ,w )); il existe naturellement des variantes dans le choix des 杻ⁱ . On définit, par induction transfinie, une relation fonctionnelle J de façon que:

On écrit J size=1^﨡 au lieu de J( 﨡). La formule L(v ) est la formule:

Elle définit dans face=F9828 M la collection L face=F9828 size=1^M.

La notion d’ensemble constructible est susceptible de généralisation. Ainsi, si a est un ensemble d’ordinaux de face=F9828 M (par exemple un sous-ensemble de l’ordinal 諸 de face=F9828 M), il existe un plus petit modèle intérieur de face=F9828 M qui contient l’objet a . Les éléments de ce modèle sont appelés ensemble constructibles à partir de a (dans face=F9828 M).

Ensembles définissables à partir d’ordinaux

Soit face=F9828 M un modèle de ZF. Un énoncé A à n + 1 variables libres et des objets a ¹, ..., a ⁿ de face=F9828 M permettent de définir la partie de M formée des éléments tels que A(a , a ¹, ..., a ⁿ ) soit vrai dans face=F9828 M. Si cette partie se réduit à un élément, cet élément est dit définissable à partir de a ¹, ..., a ⁿ . On peut ainsi considérer la collection des objets de M définissables à partir d’ordinaux. Le fait qu’il s’agit bien d’une collection dans face=F9828 M est conséquence du principe de réflexion énoncé au chapitre 3. Cette collection n’est pas transitive mais contient une plus grande collection transitive dont les éléments sont appelés ensembles héréditairement définissables à partir d’ordinaux. Cette collection forme un modèle intérieur noté HDO face=F9828 size=1^M; il en est de même des ensembles héréditairement définissables à partir d’ordinaux et de parties de N, qui forment un modèle HDO 戮(N) face=F9828 size=1^M.

Extensions génériques et forcing

La notion d’extension générique issue des travaux de Cohen, et qui s’est clarifiée notamment dans les travaux de Solovay, emprunte une direction inverse de celle qui avait été choisie jusqu’à présent: il s’agit de passer d’un modèle face=F9828 M à un modèle face=F9828 M dont face=F9828 M soit modèle intérieur; cette technique est connue sous le nom de forcing . Pour cela, fixons un modèle face=F9828 M de ZF et un ensemble (partiellement) ordonné C de face=F9828 M. Les éléments qui appartiennent au domaine de C sont appelés conditions .

D’un point de vue heuristique, les conditions peuvent être considérées comme des informations élémentaires sur l’extension qu’il s’agit de construire; une condition p est plus petite qu’une autre si elle donne plus d’information.

Un ensemble D de conditions est dense si toute condition admet un minorant dans D.

Définition. Une partie G de M formée de conditions est dite face=F9828 M-générique si les clauses suivantes sont satisfaites:

– si p est élément de G et si p minore q , alors q est élément de G;

– deux éléments p et q de G ont un minorant commun dans G;

– si D est un objet de M qui est un ensemble dense de conditions, il existe une condition p qui appartient à D (au sens de face=F9828 M) et est élément de G.

Théorème. Il existe un modèle face=F9828 de ZF qui a les propriétés suivantes:

– M est modèle intérieur de face=F9828 ;

– G est un ensemble dans face=F9828 ;

– si face=F9828 N est un modèle de ZF ayant ces deux premières propriétés, il existe une bijection de face=F9828 sur un modèle intérieur de face=F9828 N qui est l’identité sur M.

De plus, face=F9828 est unique en ce sens que deux modèles face=F9828 ¹ et face=F9828 ² ayant les propriétés ci-dessus s’échangent par un isomorphisme qui est l’identité sur M. face=F9828 est noté face=F9828 M[G].

Note : Dire que G est un ensemble dans face=F9828 , c’est dire qu’il existe un objet de N auquel appartiennent les objets de G et eux seuls.

La preuve du théorème et l’étude des propriétés de face=F9828 M[G] se font par l’intermédiaire d’une procédure de contrôle de la validité des énoncés dans face=F9828 M[G]. Cette procédure utilise une relation fonctionnelle de face=F9828 M[G] notée V^G, dont la restriction à M est une surjection de M sur face=F9828 M[G]. Le contrôle proprement dit se fait par l’intermédiaire du forcing: à tout énoncé A à n variables libres est associé un autre énoncé 塞 A comportant une variable libre supplémentaire v (ainsi que C comme paramètre). Si on interprète l’énoncé 塞 A dans face=F9828 M, la variable v étant interprétée par une condition p et v ¹, ..., v ⁿ par les objets a ¹, ..., a ⁿ de M, on obtient des assertions écrites p 塞 A(a ¹, ..., a ⁿ ) qu’on lit «p force A(a ¹, ..., a ⁿ )»; on a alors un résultat très important:

Lemme de vérité: L’énoncé A(V^G(a ¹), ..., V^G(a ⁿ ), ..., V^G(a ⁿ )) est vrai dans face=F9828 M[G] si et seulement s’il existe une condition p de G qui force A(a ¹, ..., a ⁿ ).

6. Les grands résultats d’indépendance

Le fait que l’hypothèse du continu ne puisse pas être décidée à partir des axiomes de ZF est certainement l’un des résultats mathématiques les plus profonds du XX^e siècle. Le but de ce chapitre est de montrer comment les techniques de construction de modèles décrites plus haut permettent d’établir l’indépendance de l’hypothèse du continu et de l’axiome du choix. D’autres résultats d’indépendance plus techniques sont ensuite évoqués.

La non-contradiction de l’axiome du choix et de l’hypothèse du continu

Le résultat suivant est dû à Gödel.

Théorème. Si face=F9828 M est un modèle de ZF, alors le modèle intérieur L face=F9828 M formé des ensembles constructibles de face=F9828 M satisfait l’axiome du choix et l’hypothèse du continu généralisée.

Le théorème ci-dessus constitue une preuve de la non-contradiction de ZFC à partir de celle de ZF et aussi de la non-contradiction de la théorie obtenue en ajoutant à ZFC l’hypothèse du continu, toujours à partir de la non-contradiction de ZF.

La négation de l’axiome du choix et de l’hypothèse du continu

Avant d’exposer les célèbres résultats de Cohen, on va voir comment la technique des extensions génériques permet de construire des modèles où est nié l’axiome de constructibilité 葉v L(v ), qui exprime que tout ensemble est constructible et qui est vrai dans tout modèle de la forme L face=F9828 size=1^M. On part d’un modèle face=F9828 M de ZFC qui satisfait 葉v L(v ) et, dans face=F9828 M, on considère l’ensemble des applications de domaine fini inclus dans l’ordinal 諸 à valeurs 0 ou 1 qu’on munit de l’ordre inverse du prolongement et qu’on note C. Soit G une partie face=F9828 M-générique de C.

Lemme:(1) Dans face=F9828 M[G], il existe une partie de g de N qui est telle que G soit précisément constituée des restrictions finies de la fonction caractéristique de g ,

(2) g est distinct de toutes les parties de N qui sont constructibles dans face=F9828 M[G].

On va donner la preuve du point (2) qui fournira un exemple d’utilisation des ensembles denses.

On note que les parties de N qui sont constructibles dans face=F9828 M[G] sont celles qui sont dans face=F9828 M. Soit a une telle partie et f ^a sa fonction caractéristique, l’ensemble D^a , défini dans face=F9828 M par: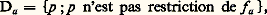

est dense et rencontre donc le générique; on en déduit immédiatement que g et a sont distincts.

La transformation du résultat ci-dessus en une preuve de la non-contradiction de la négation de l’axiome de constructibilité est subordonnée à la mise en évidence de modèles admettant des génériques.

Proposition . Si face=F9828 M est un modèle dénombrable de ZF, si C est un ensemble ordonné de face=F9828 M et si p est une condition, il existe une partie face=F9828 M-générique de C qui admet p comme élément.

Preuve . On range les parties denses de C qui sont dans face=F9828 M en une suite D¹, ..., Dⁿ , ...; on pose p ⁰ = p et on définit successivement des éléments p ⁿ de Dⁿ , p ⁿ minorant p ^n-1 ; la partie générique cherchée est formée de la réunion des majorants des conditions p ⁿ .

On vient de décrire une technique permettant en somme d’ajouter à un modèle de ZF une «nouvelle» partie de N. Pour construire un modèle de la négation de l’hypothèse du continu, on cherche à ajouter simultanément beaucoup de nouvelles parties de N.

Partons, toujours, comme plus haut, d’un modèle face=F9828 M de ZF satisfaisant l’axiome de constructibilité ; dans face=F9828 M, on définit l’ensemble ordonné C des applications de domaine fini inclus dans l’ensemble produit N 憐 尿² à valeurs 0 ou 1. Une partie face=F9828 M-générique est alors l’ensemble des restrictions d’une partie de N 憐 尿² qui est dans face=F9828 M[G]. En prenant des sections, on obtient une famille de parties de N indexées par le cardinal 尿² de face=F9828 M qui sont deux à deux distinctes. Pour conclure que l’hypothèse du continu est niée dans face=F9828 M[G], il reste à vérifier que le cardinal 尿² de face=F9828 M reste le deuxième cardinal non dénombrable du modèle face=F9828 M[G]. Ceci résulte d’une propriété générale des extensions génériques correspondant aux ensembles de conditions qui vérifient la condition d’antichaîne dénombrable (tout ensemble de conditions deux à deux incompatibles est au plus dénombrable): les cardinaux de face=F9828 M et face=F9828 M[G] sont les mêmes. L’ensemble C envisagé ci-dessus vérifie la condition d’antichaîne dénombrable.

Le modèle face=F9828 M[G] considéré à l’instant vérifie l’axiome du choix comme d’ailleurs toute extension générique d’un modèle satisfaisant l’axiome du choix. Une preuve de l’indépendance de la négation de l’axiome du choix est fondée sur le fait que l’axiome du choix est nié dans le modèle intérieur HDO 戮(N) face=F9828 M^[G]. Nous ne développerons pas la technique permettant d’établir ce résultat.

Le problème de la mesure

L’indépendance de l’axiome du choix a donné une actualité nouvelle à un type de problème déjà évoqué au chapitre 4 et consistant à déterminer si l’axiome du choix peut être éliminé de la preuve de tel ou tel théorème. À cet égard, le résultat le plus significatif est celui qui prouve que quelque forme de l’axiome du choix est indispensable à la mise en évidence d’ensembles non mesurables-Lebesgue (Solovay, 1970). On part d’un modèle face=F9828 M de ZF satisfaisant l’axiome de constructibilité et admettant un cardinal inaccessible 行; on considère ensuite un modèle intérieur d’une extension générique obtenue en «ajoutant» des surjections de 諸 sur tous les cardinaux 麗 行. Le modèle face=F9828 M obtenu vérifie une forme affaiblie de l’axiome du choix suffisante pour développer la théorie de la mesure, l’axiome des choix dépendants D.C. énoncé au chapitre 4 (cf. supra ). En revanche, dans face=F9828 M , toute partie de R est mesurable-Lebesgue. Le problème d’éliminer l’utilisation d’un cardinal inaccessible est resté longtemps ouvert; mais une réponse négative vient d’être donnée par Shelah: la non-contradiction de la théorie ZF + DC + «tout ensemble est mesurable-Lebesgue» équivaut à celle de ZFC + HI (où HI est l’hypothèse d’existence d’un cardinal inaccessible); l’hypothèse «tout ensemble est mesurable» est donc plus forte que ZF.

Le problème de Souslin et l’axiome de Martin

Les nombres réels peuvent être munis d’un ordre dense sans premier ni dernier élément et tel que toute partie non vide minorée (resp. majorée) ait une borne inférieure (resp. supérieure). Un tel ordre est appelé un continu . Tout continu qui admet une partie dense dénombrable est isomorphe à R. Appelons continu de Souslin un continu tel que toute famille d’intervalles ouverts deux à deux disjoints soit au plus dénombrable. L’hypothèse de Souslin est l’assertion: Tout continu de Souslin est isomorphe à R. La construction d’extensions génériques où l’hypothèse de Souslin est niée a suivi les premiers résultats sur le forcing. Mais la construction d’extensions où l’hypothèse de Souslin est vraie est plus délicate. S’il est relativement facile, en effet, de construire une extension générique d’un modèle face=F9828 M éliminant un continu de Souslin non isomorphe à R dans face=F9828 M, l’élimination de tous les continus de Souslin non isomorphes à R nécessite en revanche un délicat processus d’itération mis au point par Solovay et Tennenbaum (1970). Ce processus conduit à des modèles où l’hypothèse du continu est fausse. La compatibilité de l’hypothèse de Souslin et de l’hypothèse du continu a été établie par Jensen (1971) par une construction extrêmement délicate.

L’analyse du procédé d’itération de Solovay-Tennenbaum a conduit à la formulation d’une nouvelle hypothèse présentée comme une alternative de l’hypothèse du continu, appelée axiome de Martin , énoncé en 1970, et qui s’énonce:

Pour tout ensemble ordonné C et pour toute famille F de parties denses de C indexée par un cardinal strictement plus petit que celui de 戮(N), il existe une partie de C formée d’éléments deux à deux compatibles et rencontrant toutes les parties denses de F.

On remarque que l’axiome de Martin assure l’existence d’ensembles «presque» génériques. L’axiome de Martin est particulièrement fructueux, associé à la négation de l’hypothèse du continu: il implique alors l’hypothèse de Souslin et a de nombreuses conséquences en topologie générale (par exemple).

En revanche, Jensen a démontré que l’hypothèse de Souslin est niée dans l’univers L des ensembles constructibles de Gödel. Il a pu dégager de sa démonstration de nouveaux principes combinatoires portant sur les ordinaux non dénombrables qui ont leur utilité propre, servant notamment à expliciter la structure de L et à établir dans L des résultats de nature algébrique ou topologique (cf. Résultats d’indépendance en algèbre et en analyse ).

7. La pratique mathématique dans les différents modèles de ZF

Ainsi qu’on l’a noté dans l’introduction, la pratique mathématique est peu affectée par la pluralité des modèles de ZF. De nombreuses questions ne sont en effet pas sensibles aux changements de modèles; les exemples qui suivront rendront cette assertion un peu plus précise, tout en marquant ses limites.

Topologie et théorie descriptive des ensembles

La théorie descriptive des ensembles est issue des travaux de l’école de Lusin sur les ensembles analytiques et projectifs. En nous bornant aux espaces topologiques Rⁿ , rappelons que les boréliens sont les éléments de la plus petite famille de parties de Rⁿ contenant les ouverts et stable par réunion dénombrable et complémentation. Les ensembles analytiques de Rⁿ sont les projections des ensembles boréliens de Rⁿ⁺¹ ; on les appelle aussi ¹¹. Leurs compléments sont coanalytiques, ou 刺¹¹. À partir des 刺¹¹, on obtient par projection les ¹²; à partir de ceux-ci, par complémentation, les 刺¹² et ainsi de suite. Les ensembles projectifs sont tous les ensembles obtenus après un nombre fini de ces opérations. Le fait que la logique s’introduise naturellement dans la théorie descriptive tient à l’analogie entre les opérations de projection et de complémentation d’une part, le quantificateur 說 et le connecteur 囹 d’autre part. Cette analogie peut, au demeurant, être rendue précise.

L’énoncé qui suit regroupe un certain nombre de résultats importants de la théorie descriptive classique, tous antérieurs à 1938.

Théorème.

(1) Tout ensemble ¹¹ non dénombrable admet un sous-ensemble parfait non vide (et a donc la puissance du continu);

(2) tout ensemble ¹¹ est mesurable-Lebesgue;

(3) tout ensemble 刺¹¹ est réunion de 尿¹ boréliens;

(4) tout ensemble 刺¹¹ du plan est uniformisable par un sous-ensemble 刺¹¹.

Les espoirs d’étendre ces résultats aux autres ensembles projectifs ont été déçus: les analogues de (1) et (2) pour les ¹² sont contredits par l’axiome de constructibilité.

On peut également, par la méthode des extensions génériques, construire des modèles où les analogues de (3) et (4) pour des niveaux supérieurs de la hiérarchie projective sont en défaut.

L’introduction systématique de la logique dans la théorie descriptive conduit à privilégier le mode de construction d’un ensemble borélien (par réunions dénombrables et complémentations) ou d’un ensemble projectif (par projections et complémentations). Pour expliciter ce point de vue, considérons deux modèles face=F9828 M et face=F9828 de ZF tels que face=F9828 M soit un modèle intérieur de face=F9828 et donnons-nous dans face=F9828 M un ensemble analytique de nombres réels A. On prouve que A est la projection d’un fermé F de R 憐 N^N. Et à F est associé le fermé 錄 de face=F9828 qui est son adhérence. On note à la projection de 錄. Le résultat qui suit est une traduction d’un résultat métamathématique important connu sous le nom de lemme de Shoenfield.

Théorème . A est l’ensemble des réels de face=F9828 M si et seulement si à est l’ensemble des réels de face=F9828 .

Ce résultat permet, entre autres choses, d’établir que à est indépendant du choix de F.

Il se trouve que nombre de problèmes mathématiques consistent à déterminer si tel ou tel ensemble analytique est ou non l’ensemble de tous les nombres réels (c’est le cas, par exemple, du problème classique suivant: Tout opérateur continu dans un Hilbert admet-il un sous-espace invariant?). La possibilité ainsi ouverte d’utiliser un «changement de modèle» pour établir certains résultats semble donc prometteuse.

Résultats d’indépendance en algèbre et en analyse

Les travaux récents ont mis en évidence l’indépendance de certains problèmes issus non de la pratique de la théorie des ensembles (ou de la théorie descriptive) mais de celle de l’algèbre ou de l’analyse.

Citons tout d’abord le problème de Whitehead: Déterminer les groupes G tels que tout homomorphisme surjectif g d’un groupe H sur G de noyau isomorphe à Z admette une rétraction, c’est-à-dire un homomorphisme h de G dans H tel que g 獵 h soit l’identité. Les groupes dénombrables qui ont cette propriété sont précisément les groupes dénombrables libres. Le fait de savoir si cette caractérisation s’étend en cardinalité 尿¹ est indépendant des axiomes de la théorie des ensembles ZFC (même si on y inclut l’hypothèse du continu). Ce résultat, dû à Shelah (1974), met en évidence une intéressante bifurcation: l’indépendance de la conjecture est démontrée à partir de l’axiome de Martin, alors que les méthodes de Jensen montrent que la conjecture est niée dans L.

Un autre résultat frappant concerne l’existence d’homomorphismes discontinus de l’algèbre de Banach C des fonctions continues de [0, 1] à valeurs complexes sur une algèbre de Banach complexe B. Si B est précisément C, la réponse au problème est négative. En revanche, l’hypothèse du continu permet de construire une algèbre de Banach B pour laquelle existe un homomorphisme discontinu. Enfin, Solovay a exhibé un modèle générique dans lequel, quelle que soit l’algèbre B, il n’existe pas d’homomorphisme discontinu de C dans B.

8. Au-delà de ZF

De nombreux problèmes n’étant pas, comme on l’a vu, décidés par la théorie ZF, il est naturel d’entreprendre l’étude de nouveaux axiomes. Cette étude ne se limite pas à ceux qui ont, comme l’axiome de Martin, été reconnus compatibles avec ZF en ce sens qu’on a produit une preuve de non-contradiction de la théorie obtenue en les ajoutant à ZF (à partir de la non-contradiction de ZF). Elle englobe aussi l’analyse d’hypothèses plus fortes que ZF.

Grands cardinaux et théorie des dièses

La recherche d’axiomes plus forts que la théorie des ensembles s’est développée à l’origine dans la théorie des cardinaux. De nombreuses propriétés ont été étudiées et comparées, l’existence de cardinaux vérifiant ces propriétés constituant autant d’axiomes de grands cardinaux . Nous ne retiendrons ici que l’hypothèse d’Ulam , qui affirme l’existence d’ensemble infinis I tels que 戮(I) porte une mesure nulle sur les parties finies et 靖-additive. On montre que le cardinal d’un tel ensemble I est gigantesque et excède en particulier les premiers inaccessibles; l’hypothèse d’Ulam contredit l’axiome de constructibilité et a même pour conséquence que les parties de N constructibles à partir de l’une d’entre elles forment un ensemble dénombrable. Cela permet de prouver que tout ensemble ¹² est mesurable-Lebesgue et d’autres résultats sur les ¹². C’est là une des conséquences les plus frappantes de l’existence des cardinaux mesurables qui n’a guère trouvé son équivalent dans l’étude d’autres types de grands cardinaux.

L’exploration des modèles face=F9828 M de la théorie des ensembles où existent des cardinaux mesurables utilise des outils élaborés de théorie des modèles (convenablement formalisés dans face=F9828 M). C’est ainsi que, dans ces modèles, il existe une partie de N notée 0 size=1^戀凉 qui code les formules vraies dans le modèle intérieur des constructibles. Ce fait a conduit à la formulation autonome d’une autre hypothèse notée «0 size=1^戀凉 existe» et exprimant essentiellement l’existence d’une famille (non dénombrable) d’ordinaux indiscernables pour le modèle intérieur des constructibles, c’est-à-dire vérifiant les mêmes formules dans ce modèle (pour une définition précise de l’indiscernabilité, on se reportera à l’article THÉORIE DES MODÈLES). Des considérations analogues permettent d’associer à chaque partie a de N, une partie a size=1^戀凉 de N codant les formules vérifiées dans le modèle intérieur des constructibles à partir de a . On peut ainsi considérer des hypothèses du type 葉a (a size=1^戀凉 existe) qui permettent de décider certaines propositions indépendantes de ZF.

Axiome de détermination

Une autre direction de recherche de nouveaux axiomes est issue de la théorie des jeux. Considérons un jeu où deux joueurs A et B choisissent alternativement des nombres entiers; on suppose que le jeu continue indéfiniment, de sorte qu’une suite 靖 d’entiers est construite. A gagne le jeu si 靖 appartient à un ensemble X de suites fixé à l’avance. Le jeu correspondant à cet ensemble X est déterminé s’il existe une stratégie gagnante pour l’un ou l’autre des joueurs. L’axiome de détermination est l’assertion: Tout jeu est déterminé. Cet axiome contredit l’axiome du choix et implique la mesurabilité de toutes les parties de R. Certaines de ses conséquences sont plus fortes que la théorie des ensembles (existence de cardinaux mesurables) et, faute d’intuition claire, on doit considérer cet axiome avec circonspection; c’est pourquoi on a envisagé des versions affaiblies affirmant, par exemple, la détermination des ensembles projectifs. L’axiome de détermination projective a connu un certain succès en théorie descriptive. Il permet en particulier d’étendre les points (1) et (2) du théorème du chapitre 7 à tous les projectifs et le point (4) aux 刺¹²ⁿ⁺¹ .

D’autres travaux ont établi un pont entre l’étude de la détermination des ensembles et les recherches sur les grands cardinaux. C’est ainsi que Martin et Harrington ont prouvé que la détermination des jeux analytiques équivaut à l’hypothèse 葉a (a size=1^戀凉 existe). Quant à la détermination des boréliens, elle est prouvable dans ZF (Martin, 1974), mais non dans des théories plus faibles, une forme de remplacement devant être utilisée dans la preuve; c’est là le premier exemple où l’axiome de remplacement est nécessaire à la solution d’un problème qui n’est pas issu de la théorie des ensembles elle-même.

Le problème des cardinaux singuliers

Si face=F9828 M est un modèle de la théorie des ensembles ne vérifiant pas l’hypothèse généralisée du continu, il existe un premier ordinal tel que:

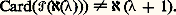La technique des extensions génériques a rapidement produit des modèles où est n’importe quel ordinal successeur. En revanche, des modèles où est 諸 ou 尿¹ n’ont pu être construits; se trouvait ainsi posé le problème des «cardinaux singuliers». L’insuccès du forcing est explicable: ne peut être égal à 尿¹ (Silver, 1974). Ce premier résultat a été suivi d’un autre, dû à Jensen, établissant que l’hypothèse = 諸 est plus forte que la théorie des ensembles (elle implique l’hypothèse 0 size=1^戀凉 existe).

Dans sa preuve (1975), Jensen a utilisé une analyse extrêmement fine de la structure des ensembles constructibles et, en particulier, des injections de l’un des ensembles J size=1^﨡 dans un autre (on se reportera au chapitre 5 pour la définition de J size=1^﨡). Le résultat de Jensen est la conséquence du fait suivant qui limite le nombre de parties d’un cardinal donné dans les modèles où 0 size=1^戀凉 n’existe pas.

Lemme de recouvrement. Soit face=F9828 M un modèle de ZFC où 0 size=1^戀凉 n’existe pas; dans face=F9828 M, tout ensemble non dénombrable X d’ordinaux est contenu dans un ensemble constructible de même cardinalité.

La méthode de Jensen constitue une approche radicalement nouvelle de la théorie des ensembles, de nature à l’enrichir encore considérablement. Il est évidemment impossible de rendre compte de la preuve du lemme de recouvrement; pour expliquer cependant le lien opéré par Jensen entre des objets de nature aussi distincte, disons qu’à partir d’un ensemble non «recouvert» on peut construire un cardinal 見 et une injection non triviale j de J size=1^見 dans un J size=1^﨡 qui préserve la validité de certaines formules; dans ces conditions, le premier ordinal 﨣 tel que j ( 﨣) 﨣 a des propriétés de grand cardinal.

Les recherches commencées par Jensen se poursuivent naturellement; pour étendre le lemme de recouvrement à des modèles où 0 size=1^戀凉 existe, ou même où existent des cardinaux mesurables, Jensen (1977) a été amené à définir un intéressant modèle intérieur K qui – pour ces modèles – se substitue à L. Dans le même temps, des modèles où = 諸 ont été construits par Magidor en utilisant des hypothèses de grands cardinaux bien plus fortes que l’hypothèse d’Ulam. Également, des lois limitant le comportement de la relation fonctionnelle F définie par:

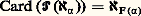ont été établies par Silver, Galvin, Hajnal et Shelah (1978); la théorie des cardinaux se révélait ainsi beaucoup plus complexe qu’on ne l’avait longtemps cru.

En conclusion, il est naturel de se demander si les recherches actuelles mettent les spécialistes en mesure de fournir des réponses aux questions que ne décide pas ZFC. Ceux des mathématiciens qui, comme Gödel, estiment que le problème du continu a une réponse déterminée sont unanimes à considérer que cette réponse doit être négative. Cela dit, la simple négation de l’hypothèse du continu n’est pas un axiome mathématiquement riche. On peut dire qu’il n’existe pas, en l’état actuel de la science, d’hypothèse plus forte que ZF, communément admise et susceptible d’enrichir et d’unifier la théorie des ensembles ou même simplement l’étude des ensembles de nombres réels. L’axiome de Martin a ses adeptes, mais ne semble guère plus riche que l’hypothèse du continu elle-même; l’axiome de détermination ou ses variantes se heurtent à une certaine méfiance. À cet égard, l’un des espoirs des spécialistes réside en la découverte éventuelle d’un lien entre l’existence de grands cardinaux et l’axiome de détermination. Sans se livrer à une maladroite «prospective scientifique», on peut dire qu’il existe des indices d’un tel phénomène de convergence entre branches distinctes. La poursuite de l’étude des modèles analogues à K paraît conduire à des modèles vérifiant quelque forme de détermination; la détermination des ensembles 刺¹² a été établie par Martin (1978) à partir d’hypothèses très fortes de grands cardinaux; enfin, Kechris et Woodin (1982) ont annoncé avoir établi un résultat d’équivalence entre la détermination et des propriétés de type grands cardinaux mais contredisant l’axiome du choix. Ainsi, la fin du siècle sera peut-être le témoin d’une certaine réunification de la théorie des ensembles.

Encyclopédie Universelle. 2012.